1. Почему она так знаменита?
Великая теорема Ферма — математическая задача невероятной сложности, и тем не менее ее формулировку может понять каждый с 5-ю классами средней школы, а вот доказательство — даже далеко не всякий математик-профессионал. Ни в физике, ни в химии, ни в биологии, ни в той же математике нет ни одной проблемы, которая формулировалась бы так просто, но оставалась нерешенной так долго.
2. В чем же она состоит? Начнем с пифагоровых штанов
Формулировка действительно проста — на первый взгляд. Как известно нам с детства, «пифагоровы штаны на все стороны равны».
Проблема выглядит столь простой потому, что в основе ее лежало математическое утверждение, которое всем известно:
Теорема Пифагора: в любом прямоугольном треугольнике квадрат, построенный на гипотенузе, равен сумме квадратов, построенных на катетах.
То есть легко подобрать множество чисел, которые прекрасно удовлетворяют равенству х2 + y2 = z2. Начиная с 3, 4, 5 — действительно, младшекласснику понятно, что
9+16=25.
Или 5, 12, 13:
25 + 144 = 169.
Замечательно. Ну и так далее.
А если взять похожее уравнение х3+ y3 = z3? Может, тоже есть такие числа? И так далее.
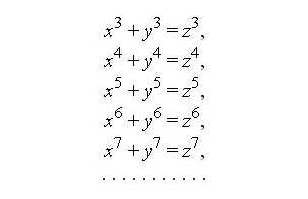
Так вот, оказывается, что их НЕТ.
Вот тут начинается подвох. Простота — кажущаяся, потому что трудно доказать не наличие чего-то, а наоборот, отсутствие. Когда надо доказать, что решение есть, можно и нужно просто привести это решение.
Доказать отсутствие сложнее: например, некто говорит: такое-то уравнение не имеет решений. Посадить его в лужу? Легко: бац — а вот оно, решение! (приведите решение). И все, оппонент сражен.
А как доказать отсутствие? Сказать: «Я не нашел таких решений»? А может, ты плохо искал? А вдруг они есть, только очень большие, ну очень, такие, что даже у сверхмощного компьютера пока не хватает силенок? Вот это-то и сложно.
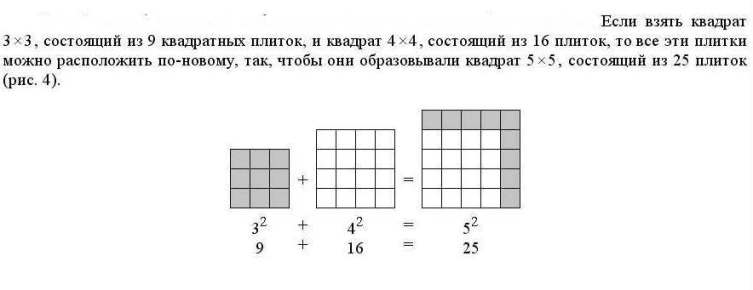
В наглядном виде это можно показать так: если взять два квадратика подходящих размеров и разобрать на единичные квадратики, то из этой кучки единичных квадратиков получается третий квадратик:
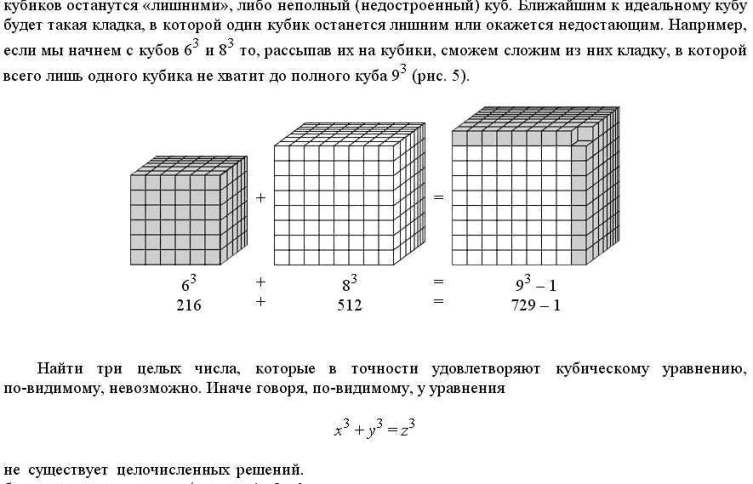
А проделаем то же с третьим измерением (рис. 3) — не получается. Не хватает кубиков, или остаются лишние:
3. История: более 350 лет поиска решений
Теорема была сформулирована Пьером Ферма в 1637 году на полях книги «Арифметика» Диофанта с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы его можно было здесь поместить:
Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него.
Несколько позже сам Ферма опубликовал доказательство частного случая для n = 4, что добавляет сомнений в том, что у него было доказательство общего случая, иначе он непременно упомянул бы о нём в этой статье. Эйлер в 1770 году доказал теорему для случая n = 3, Дирихле и Лежандр в 1825 году — для n = 5, Ламе — для n = 7. Куммер показал, что теорема верна для всех простых n, меньших 100, и так далее.

Но все это были частные случаи, а не универсальное доказательство для ВСЕХ ЧИСЕЛ.
Над полным доказательством Великой теоремы работало немало выдающихся математиков, и эти усилия привели к получению многих результатов современной теории чисел.
Считается, что Великая теорема стоит на первом месте по количеству неверных доказательств. Многие начинающие математики считали своим долгом подступиться к Великой теореме, но доказать ее все никак не удавалось.
Сначала не удавалось сто лет. Потом еще сто. Среди математиков стал развиваться массовый синдром: «Как же так? Ферма доказал, а я что, не смогу, что ли?», и некоторые из них на этой почве свихнулись в полном смысле этого слова.
Некоторые пытались прославиться от обратного: доказать, что она не верна. А для этого, как мы говорили, достаточно просто-напросто привести пример: вот три числа, одно в кубе плюс второе в кубе — равно третьему в кубе. И они искали такие тройки чисел. Но безуспешно… И никакие компьютеры, ни с каким быстродействием, никогда не смогли бы ни проверить теорему, ни опровергнуть ее, ведь все переменные этого уравнения (в том числе и показатели степени) могут возрастать до бесконечности.
4. Наконец-то!
Наконец 23 июня 1993 года в Кембридже состоялась самая важная лекция по математике в ХХ веке. Лектором был Эндрю Уайлс, англичанин, профессор Принстонского университета. Эндрю Уайлс продемонстрировал ученым полное доказательство Великой теоремы Ферма.
Он шел к этому 30 лет, буквально с десятилетнего возраста. Его доказательство потом еще было уточнено и усовершенствовано в 1995 году, но самое главное — Великая теорема была доказана!
На это человечеству понадобилось 358 лет. Для доказательства была применена «самая высшая» и самая современная математическая наука. Поэтому изложить это доказательство в рамках заметочки никак нельзя, и читателям придется поверить на слово мне, математикам Кембриджа и Принстона и так далее.
Это доказательство закрыло сразу две страницы истории математики: 350-летний поиск доказательств Великой теоремы и бесконечные нашествия ферматистов на все математические кафедры всех университетов и институтов в мире.
5. Кто такие ферматисты?
Как сказано выше, формулировка Великой теоремы очень проста и понятна, поэтому есть стойкая иллюзия, что и доказательство ее также должно быть простым, понятным и вкладываться в знания алгебры в объеме 5−6 классов. Это породило неисчислимые толпы жертв фанатизма, называемых ферматистами, которые пытались ее доказать, думали, что доказали, и атаковали кафедры и отдельных ученых с исписанными тетрадками в клеточку наперевес. Как все фанатики, они нетерпимы к критике, полны намерений снести все преграды и страшно самоуверенны. Обычно их толстые труды сразу выбрасывают или дают студентам кафедры теории чисел для поиска ошибки в качестве упражнения.
Как правило, все доказательства сводятся к нехитрым алгебраическим преобразованиям: там прибавил, тут вычел, возвел все в квадрат, извлек квадратный корень, свернул по формулам сокращенного умножения, применил бином Ньютона — и вот оно, доказал.
Интересно, что бОльшая часть доморощенных ферматистов даже не понимает сути теоремы — они доказывают не то, что уравнение с показателями степени больше 2 не имеет целых решений, а просто пытаются доказать, что х в степени N + y в степени N равно z в степени N, что, как вы уже, я надеюсь, понимаете, лишено всяческого смысла.
И ведь доказывают! Ошибка, как правило, возникает при очередном возведении уравнения в квадрат и последующем извлечении корня. Казалось бы: возвели в квадрат, потом извлекли корень — так на так и получится, но они всегда забывают о том, что х в квадрате и (минус х) в квадрате равны. Это элементарно, Ватсон!
Кафедры отбивались, как могли.
Учёный секретарь одного из московских академических институтов, не избежавшего нашествия ферматистов, однажды был в отпуске в Молдавии и на рынке купил какую-то снедь, которую ему завернули в местную газету.
Вернувшись с рынка, он стал просматривать этот листок и наткнулся на заметку, в которой сообщалось, что местный школьный учитель доказал теорему Ферма, и, как следствие, пелись всякие дифирамбы высокому уровню областной науки.
Учёный секретарь вырезал эту заметку, а по возвращении в Москву вставил её в рамку и повесил на стену своего кабинета. Теперь, когда на него «нападал» очередной ферматист, он широким жестом приглашал того ознакомиться с «текущим положением дел». Жизнь явно стала легче. (Саймон СИНГХ, «ВТФ»).
Я думаю, после всего, что между нами было, читатели уже смогут оценить попавшуюся мне как-то на кафедре в куче таких рукописей, тетрадок и бандеролей телеграмму:
ДОКАЗАЛ ТЕОРЕМУ ФЕРМА ТЧК ИКС СТЕПЕНИ Н ПЛЮС ИГРЕК СТЕПЕНИ Н РАВНО ЗЕТ СТЕПЕНИ Н ТЧК. ДОКАЗАТЕЛЬСТВО ДВТЧ ПЕРЕНОСИМ ИГРЕК СТЕПЕНИ Н ПРАВУЮ ЧАСТЬ ТЧК ПОДРОБНОСТИ ПИСЬМОМ




О знаменитой теореме Ферма.
Простая по внешнему виду, в общем виде теорема была сформулирована и якобы доказана (доказательство не сохранилось) Пьером Ферма в 1637 году. В последующие 358 лет теорему так и не удалось доказать. И только в 1995 году американский математик Эндрю Уайлс доказал теорему. Его 130 страничное доказательство было опубликовано в журнале «Annals of Mathematics».
Однако доказательство теоремы, предложенное им, настолько сложное, что даже немногие специалисты могут в нем разобраться. Да и теории вычетов, на которой основано доказательство теоремы, во времена Ферма еще не существовало. Наоборот, теория вычетов появилась из теоремы Ферма. Кроме того, доказательство ограничено количеством слагаемых равным 2. Большее количество слагаемых является непреодолимым для предложенным Уайлсом методом доказательства.
В настоящее время найден иной способ доказательства теоремы Ферма. Он опубликован в электронном журнале «Форум молодых ученых» №9(25) по адресу: http://forum-nauka.ru/domains_data/files/25/Solovev%20A.B..pdf
Способ доказательства, приведенный в статье, основан не на теории вычетов и позволил рассматривать числовые равенства в более широком диапазоне, с любым количеством слагаемых в обеих частях равенства. Думаю, что именно этим способом Ферма мог доказать и доказал свою знаменитую теорему.
Соловьев Анатолий Борисович
0 Ответить
Анатолий и Вера Соловьевы, здравствуйте! Рассмотренный в Вашей работе подход к разъяснению теоремы Ферма весьма интересен и познавателен! Однако, в приложении 2 содержится утверждение о том, что "...левая часть числового равенства представляет собой целые числа. Следовательно и правая часть также является целым числом. Это означает, что частное от деления произведения (BDE) на целое число F также является числом целым." Считаю это утверждение неверным, поскольку частное от деления целых чисел может принимать как целые, так и дробные значения.
0 Ответить
Я пытаюсь разобраться в некоторых вещах...и натыкаюсь на "это всем известно" "младшекласснику понятно, что "...Я не понял, вообще. по моему мнению автор не умеет объяснять
Оценка статьи: 1
0 Ответить
Мне бы Ваш проблемы, К.Ю. ? Я вон недавно в тоске ожидания сделал "открытие" на телефонном наборе цифр.
123
456
789
0
И оказалось,что "кругом по 30": сумма первой и третьей строчки, сумма первого и третьего столбика, а так же по диагоналям. Ещё меня очаровывает Фибоначчи своим рядом, который "стреляет" в идеальные пропорции формата картин и в архитектуре. Для меня, как ни бились преподы, осталось непонятным наполнение мнимого числа, которое получается из крадратного корня из -1.
Оценка статьи: 5
0 Ответить
А что - вполне знаковая статья дня. Есть над чем подумать.
От интересных, но мало полезных рассуждений, только потому что с претензией, про математику вчера, и до сегодняшних плясок идиотов, которые уже и нюх потеряли в своём ткачестве.
Понятное дело, коммерция и посещение. Только мне кажется, надо придумать внутреннее ограничение. Чтобы не просто "+16", а типа, "пройди тест на вменяемость".
Тесты есть и они очень простые. Я тут на многих, так или иначе, их проверял.
Проще сказать, - и это врачебная тайна - кто прошёл. А вот остальные...))
0 Ответить
Ну статья,конечно в чём-то хамская по отношению к "ферматистам"-ведь автор сам пишет и тут же забывает,что Ферма тоже её не доказал т.е Ферма попадает в группу "дил-
летантов"-"ферматистов".И это несмотря на то ,что Ферма
является одним из основоположников мат.анализа.Т.е в отличие от Уоллеса и др. "специалистов" "кое-что" в математике соображал и для неё сделал.А жонглирование мат. структурами за гос.счёт всё равно мозгов прибавить не может.
0 Ответить
Уравнение Ферма. a^n+b^n=c^n b=a+x c=a+x+y a^n=(a+x+y)^n-(a+x)^n
a^n=n(n+1)/2 (n+1)(n+2)/2=n(n+1)/2 n=n+2 ?и получаем n=-1 n=1 n=2 из чего следует a^n+b^n=c^n при n=-1 n=1 n=2 имеет множество решений
0 Ответить
(а+x+y)^n-(a+x)^n= ?
0 Ответить
(a+b)^n= ? (a^n-b^n)/(a-b)= ? (a-b)^2n= ?(a-b)^(2n+1)= ?
( a^(2n+1)+b^(2n+1) )/(a+b)= ? осталось меньше 43.5часов
0 Ответить
a^n+b^n/a+b ответа нет,но a^2n+1+b^2n+1/a+b=x х равен целому числу или a^2n+b^2n/a+b=x+y/(a+b) y
0 Ответить
что можно доказать на 130 страницах,только завести в лабиринт ха=ха в периоде.
0 Ответить
нонсенс!теоремы нет!!!это просто уравнение,а оно требует решение но не доказательство!!!
0 Ответить
Ферма вроде читал арифметику.Но он не прав утверждая что поля книги слишком малы.На полях 2 страниц нормальной книги эту теорему можно доказать.Доказательство представлю 9 мая в 1.00 по Москве.А пока решите уравнение (a^n+b^n)/(a+d)=?
0 Ответить
читать дальше →
1 Ответить
читать дальше →
0 Ответить
Валерий Широков, Ваше выступление здесь окончено. Комментарии будут удаляться, хотя читать их весело.
1 Ответить
Марианна Власова,здоровья вам и процветания.Не смотря на то, что вы пригрозили меня удалять, я всё же рискнул ещё раз появится в вашем блоге.Я стал админом на одном научном сайте в ВК. Сожалею, не могу напечатать вам здесь ссылку. Ваши правила не позволяют это делать.Увы. Маленькая ошибка в формулировке теоремы Ферма(К.Ю.Старохамской)позволило мне вас слегка по-троллить.Не обижайтесь на меня пожалуйста.Свергать Ферма с пьедестала не собирался. Но вот вам прикол про теорему Ферма.Надеюсь шутку вы оцените.)
Дорогие читатели паблика. Вы все знаете знаменитую теорему Ферма.
Она выглядит так.
А^n + В^n = С^n
И гласит, Что при n больше двух, это равенство в целых числах не возможно.
(ЗНАЧОК ^ это степень, для тех, кто не понял.)
Англичанин Майлс(Уайлс) доказал эту знаменитую теорему. Да она верна!
Вот, теперь, зная, что она эта теорема верна, сможете ли вы доказать похожие теоремы.
А^n - В^n = С^n
При каких n и при каких целых А,В,С возможно это равенство.
Если это возможно, и вы это докажете, то можете назвать эту теорему своим именем.
Ну и ещё что-то похожее.
А^n=В^(n+1)
А^n=В^(n-1)
Ну на двух последних равенствах, условия сформулируйте сами.)))
БУДУТ ЛИ ЭТИ ТЕОРЕМЫ, ТЕОРЕМАМИ ФЕРМА, ИЛИ ВЫ ИМЕЕТЕ ПРАВО НАЗВАТЬ ИХ СВОИМ ИМЕНЕМ
НУ И ВОТ ВАМ ПРИКОЛ))
А^n - В^n = С^n
А^n = С^n + В^n
С^n + В^n = А^n
А^n+В^n=С^n
Так как у нас, А, В, С, любые числа, то мы получили, две совершенно тождественные записи с точки зрения алгебры. Отсюда следует вывод, что плюс и минус тождественны.)))))))))
0 Ответить
Марианна Власова, хочется вас спросить. Вы являетесь доктором физико- математических наук? Вы кончили МГУ? Возможно и кончили, но не физико- математический факультет. Ваши возражения типа:,,... Вы не разбираетесь в математике ...,, - есть ваше оценочное суждение. На чём оно основано? Да возможно я не разбираюсь в математике. Но в доказательство вы приводите ЧТО??? Вы уже второй раз пытаетесь задавить меня, авторитетами, и навешиванием ярлыков. Математики - они обычно доказывают. Нет - конечно требовать от вас доказательство Эйлера на этой стене - будет слишком. Но я вам привёл пример с водой. Вообще - это ТОПОЛОГИЯ. Вы начинаете мне говорить о континууме и прочее мало представимых вещах. К.Ю однако часть( только часть идеи об общем модуле( мере) в любом множестве- УХВАТИЛА!!!В ТОПОЛОГИИ теорема Ферма возможно будет звучать в других терминах. Но по сути - это будет та же теорема Ферма. Вы упёрлись в целые числа. Но числа( цифры, иероглифы)- это всего лишь знаки которым мы придаём смысл, пытаясь найти смысл в отношениях( связях) между этими иероглифами. Топология как раз и освобождает от излишних наслоений и исследует базовые , радикальные свойства математических объектов. А из всего выше сказанного раньше см гифку( любой бесформенный объём воды мы можем превратить в кубик. Вам это надо доказывать??) И два объёма воды будут равны третьему. Два кубика - в сумме дадут третий кубик.И этот факт бросает тень на доказательство Эйлера. Пока только тень. Я не собираюсь доказывать и переплёвывать Майлса. Но, то что японец покончил с собой( может он увидел что не прав) тоже наводит на размышления. Я ведь не утверждаю - что теорема Ферма- верна или не верна.( чего вы так приужахнулись?) Я пытаюсь вам показать( ЛЕГКО), что два кубика воды в сумме дают третий кубик. И вас это раздражает? По существу вы пока ничего не возразили. Ваши обвинения и доказательства - напоминают раздражения учительниц, против умного ученика. Типа он не понимает( это не доказательство) или типа?:,,... Умный -очень...,,
0 Ответить
Валерий Широков, я являюсь выпускницей физико-математической школы и факультета прикладной математики и механики Ташкентского государственного университета. Но это неважно, так как любой школьник знает: если в задаче требуется найти решение, являющееся целым числом, то нецелое число - неверный ответ.
И здесь никакие математики ничего доказывать не будут, здесь обсуждается познавательная статья.
0 Ответить
Марианна Власова, привет от мехмата Одесского университета
0 Ответить
КАРТИНКУ РАЗМЕСТИТЬ НА ЭТОЙ СТЕНЕ НЕ ВОЗМОЖНО ПОЭТОМУ КАРТИНКА НА МОЕЙ СТЕНЕ , НА МОЕЙ СТР
0 Ответить
Валерий Широков,
1. Не пишите капслоком.
2. Картинку разместить можно, и я поместила ее в Ваш комментарий.
3. Формулировка теоремы Ферма:
Для любого натурального числа n>2 уравнение
x^n+y^n=z^n
не имеет решений в целых ненулевых числах x,y,z.
0 Ответить
Марианна Власова, кстати, нечаянно наш Диоген высказал интересное следствие из ТФ - что невозможно найти единицу измерения, которая все три кубика "из воды с цементом" выразит в целых числах. Я как-то не задумывалась об этом с такой стороны.
0 Ответить
К. Ю. Старохамская, Уважаемая К. Ю. вообще то это перенормировка. Для простоты возьмите диофантовы тройки. Хотя бы волшебные 3, 4, 5.Корень кубический из 25 и будет такой мерой? Согласен, согласен, согласен!!! Это ещё надо доказать!!))Возможно в результате появятся иррациональные числа с бесконечным числом знаков. Но пример с водой - более чем нагляден. Воду ещё можно заморозить. Но нам достаточно мысленного эксперимента. Не будем заморачиваться на добывание цемента. Тем более , что вы наглядно увидели, что объём воды можно легко превратить в куб.(Ведь это у вас не вызывает желания доказывать. Это очевидно и тривиально)Вы ведь пользуетесь десятичными и натуральными логарифмами. У одного в основании стоит 10, а у другого число e которое как и пи огромно. Т.е мера, модуль может быть любой. Не обязательно целым числом. А если взять другую систему счисления, двоичную, троичную и т.д. Теорема Ферма - что нам по этому поводу скажет?? А если перейти к тройным интегралам? Сумма двух тройных интегралов, будет равна третьему тройному интегралу. Это, я сейчас, как бы перенормировал теорему Ферма для кубов. Скажете не возможно? Но с водой ведь это наглядно получилось)))).Опять слышу возражения.( заранее), что там дискретные числа( количество), а интегралы вроде как бесконечно малые. Но упростите задачу, перейдите к объёмам шаров. Объём двух шаров, в сумме даст объём третьего шара. Как найти меру для этих шаров? Да просто заполнить любой шар маленькими тестовыми шариками, конечного объёма. И вы ЛЕГКО перейдёте от возникающих бесконечностей(бесконечно малых) к счётному количеству. К счётному множеству к вашим любимым рациональным числам. Это тоже будет теорема Ферма. Но у меня вот тут и возникают сомнения. Что -то типа интуиции и здравого смысла говорит, что может перенормировка поможет??
0 Ответить
Валерий Широков, Ваши предположения наглядно доказывают, насколько Вы не разбираетесь в математике... читать дальше →
"Это тоже будет теорема Ферма." - нет!
0 Ответить
Марианна Власова, ,,….Наоборот, невозможно разложить куб на два куба …,,,Это цитата из этой статьи. К.Ю Старохамская, может конечно обвинить меня во флуде и не понимании. В ответ я могу её обвинить в неумении вести дискуссии, и в навешивании ярлыков, и оскорблении собеседника. Но факт - два куба в сумме дают третий. А теорема Ферма утверждает - это невозможно. Кто нам мешает добавить цемента в воду и получить в реале два кубика, в сумме равным третьему. Или для вас это не очевидно? Согласен, стороны этих кубиков не будут выражаться в целых числах сантиметров, миллиметров, дюймов и пр.Но кто нам мешает найти кубическую единицу( назовите хоть чебурашкой кубической)которой можно было бы измерить все три кубика? Вопрос можно ли найти такую меру?К. Ю может вы слышали об аналоговых и дискретных сигналах? Вода конечно не цифры. Но можно представить воду как множество, без привязки к свойствам цифр. Или корректнее сформулировать Ферма для n= 3.
0 Ответить
Валерий Широков,
Вся фишка в том, что эти три куба нельзя измерить одной линейкой так, чтобы результат измерений был целым. Для одного куба, как минимум, потребуется своя линейка с другими делениями.
В природе много удивительных вещей.
Так же, как и число "пи" - отношение длины окружности к радиусу - оно бесконечно, хотя свернуть окружность из листа бумаги может даже ребенок. А потом отрезать от него кусочек, равный радиусу.
0 Ответить
Валерий Широков, цитата, которую Вы привели, не просто из статьи, а из Ферма. Ферма уже всё сформулировал, и здесь речь именно о том, что формулировал он, а не Вы.
Ферма уже всё сформулировал, и здесь речь именно о том, что формулировал он, а не Вы.
0 Ответить
Марианна Власова, я не буду говорить, что товарищ не понимает разницы между натуральными числами и континуумом. Что теорема Ферма верна для натуральных чисел, а не для объема воды. Там, похоже, не надо дискутировать, а то не обобраться флуда безо всякого толка.
0 Ответить
ВСЕМ - ЗДРАВСТВУЙТЕ И ПРОЦВЕТАЙТЕ! Хочу привести именно контр - пример для n=3. Это теорема Пифагора для визуалов. НО!! Здесь уже не абстрактные цифры, а объёмы воды. И что нам мешает слить воду из одной площади в кубическую баночку????ВОТ ВАМ ДВА КУБА - ПОРОЗНЬ РАВНЫ ТРЕТЬЕМУ!!!А в этой статье утверждается, что ЭТО НЕ ВОЗМОЖНО Да - возможно это будет не в целых числах. Но кубики( объёмы воды) они реальны в отличие от цифр. Иначе следует вывод- ЧТО ЛЮБОЙ ОБЪЁМ ВОДЫ МЫ НЕ МОЖЕМ СЛИТЬ В КУБИЧЕСКУЮ БАНОЧКУ!!!И как видите два куба - в сумме дают третий. И НЕ НАДО ЗАУМНЫХ ФОРМУЛ.!!!
0 Ответить
Статья неплохая, но я не вполне поняла анекдот про заметку в рамочке. Видимо, он про и для "чайников", уверенных в том, что у теоремы Ферма может быть одно и только одно доказательство.
На самом деле у любой теоремы может быть несколько доказательств, построенных на совершенно разных принципах. Наличие одного доказательства не исключает существования множества других, причём другие доказательства могут оказаться гораздо короче, проще и элегантнее первого.
0 Ответить
В истории с рамочкой речь шла о маньяках, атаковавших кафедры. Для них факта существования какого-то доказательства было уже достаточно, чтобы они перестали мучать ученых




1 Ответить
Спасибо огромное за познавательную статью.
Хотя я и не с большим энтузиазмом работаю с цифрами, и в принципе по складу никогда не проявляла особого интереса к математике, статью прочла на одном дыхании.
И всегда с огромным интересом и уважением относилась к людям, которые умеют грамотно оперировать цифрами.
0 Ответить
Возможно, вам еще не попадалась еще "Леденящая тайна числа Пи" - тоже на сходную тему.
0 Ответить
Блеск!
Оценка статьи: 5
0 Ответить
Спасибо за очередную интересную статью!
Хочу еще добавить, что Великая теорема Ферма принесла много несчастий связанным с ее доказательством людям. Из огромного количества банально свихнувшихся в тщетных попытках поиска доказательства, хочу выделить японского математика Танияму.
Дело в том, что Уайлс, строго говоря, доказал не саму Великую теорему Ферма, а частный случай теоремы Таниямы. Ранее было доказано, что если верна теорема Таниямы (точнее, один из частных ее случаев, который и доказал Уайлс), то верна и Великая теорема Ферма. Сам же Танияма, сформулировавший теорему, названную его именем, покончил жизнь самоубийством. Читал, что сам он считал, что доказал теорему (тогда еще гипотезу) Таниямы, но его не поняли коллеги. Подруга его последовала за ним через непродолжительное время, чтобы выполнить обещание всегда быть вместе.
Оценка статьи: 5
0 Ответить
вау!!.. ну и ну.. из-за чего люди готовы расстаться с бесценным даром- с жизнью- всего лишь из-за каких-то там циферек.. елки палки.. точно крыша у них поехала!!,.. хоть они были и интеллектуалы.. но явно не в себе.. печально..
0 Ответить
Я как раз чайник, хоть обязательный курс высшей математики плю математических методов в управлении прошла в вузе и даже "сдалась" на отл. Читала с интересом, хоть сбивалась в неуместные гуманитарные вопросы и ассоциации. Последняя возникла в связи с финальной телеграммой. Пардон, анекдот: Нобелевскую экспедицию когда искали, объявили, что почтовые отправления по этому вопросу - бесплатны.Вот один заводчик другому и отбивает телеграмму: Ищите Нобеля найдете не найдете отправляйте два вагона сахарного песка вторник
Оценка статьи: 5
0 Ответить
ДОКАЗАТЕЛЬСТВО ДВТЧ ПЕРЕНОСИМ ИГРЕК СТЕПЕНИ Н ПРАВУЮ ЧАСТЬ ТЧК ПОДРОБНОСТИ ПИСЬМОМ


Первым "ферматистом" был сам Ферма. У него тоже на полробности полей не хватало.
А вообще захватывающе интересно!
Оценка статьи: 5
0 Ответить
А письмо-то с "подробностями" пришло?
Оценка статьи: 5
0 Ответить
А письмо-то с "подробностями" пришло?
нет... наверное перехватили санитары.
0 Ответить
Почему-то ферматисты вызывают у меня чувство глубокой симпатии )
)
А если брать дробные числа, то тоже никак не сходится?
Оценка статьи: 5
0 Ответить
Речь идет только о целых.
0 Ответить
увлекательно Это я и о содержании, и о манере изложения. Спасибо
Это я и о содержании, и о манере изложения. Спасибо
Оценка статьи: 5
0 Ответить
Я думаю, после всего, что между нами было
Ну конечно, теперь я, как честный человек, обязан поставить вам 5-рку.
Оценка статьи: 5
0 Ответить
Вот! Высокая Наука - она свое берет.
0 Ответить
Понятно написанный математический детектив для чайников. Читатели должны оценить! Очень хороши для понимания проблемы рис. 2 и 3. Только если "раскрыть" фото, там скрываются рис. под №№ 4 и 5. Подкорректируйте картинки.
Оценка статьи: 5
0 Ответить
Подправила с номерами и даже добавила еще картинку для увеселения последней части.
0 Ответить
Спасибо, подправлю
0 Ответить