Вначале рассмотрим классический алгоритм построения, осуществляемый в два этапа. Первый шаг построения — проведение биссектрис углов треугольника (достаточно задействовать всего два угла) для определения центра окружности. На втором этапе определяется радиус вписанной окружности. Из точки пересечения биссектрис проводится перпендикуляр к одной из сторон треугольника. Длина полученного отрезка равна искомому радиусу. Раствором циркуля равным этой величине строится вписанная окружность. Не сложно подсчитать минимальное количество проведенных линий в данном построении. Их всего 12, по 4 на построение двух биссектрис, 3 — на перпендикуляр и одна собственно на проведение самой окружности.
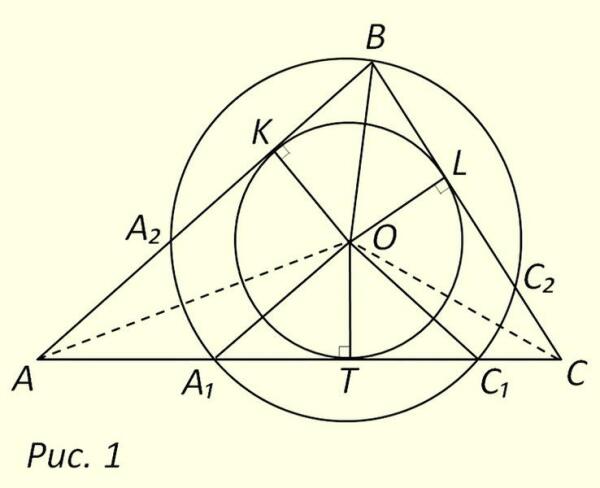
Второй вариант построения базируется на окружности, проведенной из инцентра треугольника через вершину одного из его углов, позволяющей определить местоположение точек касания вписанной окружности. Пусть в треугольник АВС (см. рис. 1) вписана окружность с центром О на пересечении биссектрис углов, А и С. Соединим точки ее касания K, T и L сторон треугольника с инцентром. Согласно свойству касательной проведений к окружности, отрезки ОК, ОТ и ОL равны радиусу окружности и перпендикулярны сторонам треугольника.
Проведем дополнительно окружность из точки О радиусом ОВ
Соединим инцентр треугольника с концами хорды А1С1. Прямоугольные треугольники А1ОТ и С1ОТ равны согласно тому, что гипотенузы А1О и С1О радиусы дополнительной окружности, а катет ОТ — общий. Следовательно точка Т середина, а ТО серединный перпендикуляр хорды А1С1. Аналогичным образом доказывается: ОК и ОL серединные перпендикуляры к двум другим хордам. Таким образом, середины хорд являются точками касания вписанной в треугольник окружности.
В треугольниках АОВ и АОС1 стороны ОВ и ОС1 радиусы дополнительной окружности, АО общая сторона и биссектриса угла ВАС. Тогда согласно равенству этих треугольников, отрезок АС†равен стороне АВ. В свою очередь отрезок А1С равен стороне ВС, ввиду сходного равенства треугольников А1ОС и ВОС.
Следствием вышеизложенного является возможность построения крайних точек хорды на стороне треугольника путем засечек дугами радиусами равными боковым сторонам из вершин прилежащих углов. Затем из вершины противолежащего стороне угла на одной из боковых стон откладывается длина второй хорды. Точка пересечения серединных перпендикуляров к полученным хордам — центр вписанной окружности.
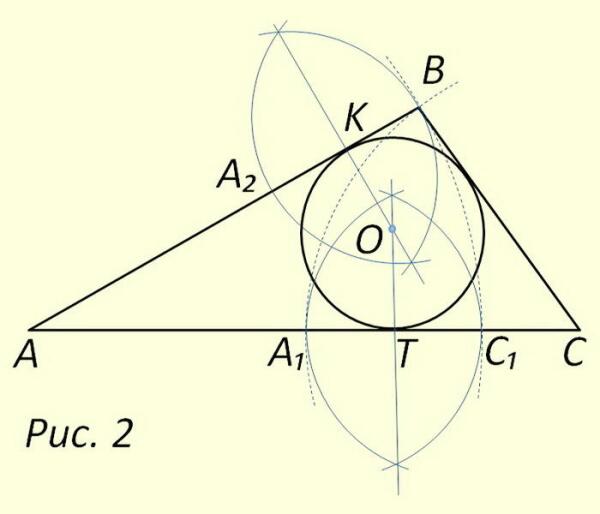
Построение в произвольно заданный треугольник АВС вписанной окружности изображено на рис. 2. На стороне АС (наибольшей, как на наиболее удобной) из вершины, А дугой радиусом АВ делаем первую засечку в точке С1, а из вершины С дугой радиусом СВ — вторую в точке А1. К полученному отрезку А1С1 восстанавливаем серединный перпендикуляр. Раствором циркуля равным А1С1 из вершины В проводим дугу пересекающую например, сторону ВА в точке А2. Тем же раствором циркуля из точки А2 через вершину В опишем вторую дугу. Соединяем точки пересечения дуг прямой, получаем второй серединный перпендикуляр. Из точки пересечения перпендикуляров радиусом равным ОТ опишем искомую вписанную в треугольник окружность.
Определим количество линий примененных в данном построении. Пять на восстановление первого серединного перпендикуляра, три линии для второго и одну на проведение вписанной окружности. Всего девять. Если сравнивать два метода построения вписанной окружности по этому показателю — преимущество за последним.
Заключительный вывод: предлагаемое построение следует рассматривать в обучении наряду с общеизвестным методом.

Карл-Август Аванти, я просто прошу Вас продолжить эту тему, в таком ракурсе. Очень тяжело преподавать этот предмет. Знаю на примере жены,...