Леонардо Пизанский. Что придумал счастливчик?

Следовательно, Леонардо — сын счастливчика, и сам был счастливчиком. А вообще был он купец и сын купца и жил в итальянском городе Пиза в XII веке.

XII век — время расцвета Пизы. Пизанцы больше сотни лет отвоевывали Средиземное море у арабов. В результате непрерывного ряда войн христиане вернулись на Сардинию и Корсику. Вслед за венецианцами моряки Пизы оказались в Константинополе, а в Египте и в Алжире — даже раньше конкурентов из Венеции.

Леонардо дома не сидел. Вместе с отцом побывал он и в Египте, и в Сирии, и в Византии. Через Византию и через Египет в Европу поступали восточные товары. Ткани, пряности и драгоценности Востока очень ценились, пизанские корабли без устали пересекали Средиземное море, богатство города и его жителей прирастало.

Леонардо Пизанский вывозил с Востока не только дорогие товары. Он знал арабский язык. В арабском переводе Фибоначчи читал трактаты античных и индийских математиков. Эти трактаты в те времена без устали размножали в библиотеках Багдада. Все, что он узнал, Леонардо обобщил в первом в средневековой Европе математическом труде, который называл «Книгой абака». Абак — это древнеримские счеты, остававшиеся и во времена Фибоначчи главным «компьютером».

В своей книге, в частности, Фибоначчи сообщил европейцам о десятичной системе счисления, которую арабы переняли у индийцев. Привычная и понятная нам позиционная система счисления, позволяющая для написания любого, сколь угодно большого числа, обойтись всего десятью цифрами, была для европейцев того времени откровением. До тех пор они пользовались римскими цифрами. При такой записи чисел даже сложение и вычитание превращались в хитроумные трюки, умножение же и деление были попросту высшим математическим пилотажем, не каждому доступным.

«Книга абака» включала в себя все известные на тот момент знания по арифметике и алгебре. Другая книга Фибоначчи, «Практика геометрии», была сводом знаний по геометрии. Обе книги выдержали испытание временем. Едва ли не четыре сотни лет они были главными учебниками математики в Европе.

В «Книге абака» Фибоначчи описывает и свое собственное математическое изобретение — числовой ряд, в котором каждый последующий член равен сумме двух ему предшествующих.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 …

Этот ряд — решение задачи о потомстве двух кроликов, сформулированной самим же Фибоначчи.

Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?

Числа этой последовательности называются числами Фибоначчи. Названа она так только в XIX веке, 700 лет спустя после кончины Леонардо Пизанского. Название это ввел в употребление французский математик Франсуа Люка́ (фр. François Édouard Anatole Lucas; 1842 —1891).

Он же определил, что возможно бесконечное число других последовательностей чисел, определяемых таким же правилом, как числа Фибоначчи: каждый последующий член в последовательности равен сумме двух членов, ему предшествующих. Если задать другую пару начальных чисел, получается другая последовательность. Так, если два первых члена этой последовательности будут числа 2 и 1, получается последовательность чисел другого вида:

2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, …

Эта последовательность чисел называется числами Люка.

С точки зрения математиков последовательность чисел Фибоначчи очень интересная. Одна из главных ее особенностей — отношение каждого последующего члена этого ряда к предыдущему неуклонно приближается к числу 1,618.

«Волшебное» это число известно с античных времен и называется еще «золотым сечением». Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок относится к большей части так, как сама большая часть относится к меньшей. Еще древнеегипетские и древнегреческие архитекторы установили, что если пропорции здания соответствуют золотому сечению, здание кажется нам красивым. Мало того, что кажется, оно и в самом деле оказывается наиболее устойчивым.

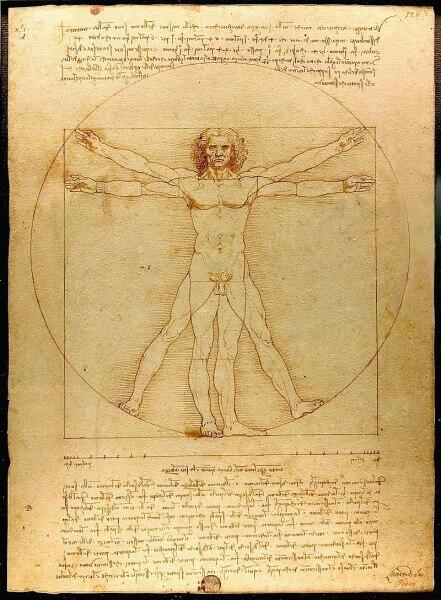
Да и пропорции человеческого тела соответствуют этой странной цифре. Этот факт демонстрирует всем известный рисунок Леонардо да Винчи — фигура человека, помещенная в круг. Расстояние от ног человека до пупа (центра тела) и от пупа до головы находятся между собой в «золотой пропорции».

Более того, многие существующие в природе спирали — рога животных, морские раковины, даже космические галактики — образуются как последовательность окружностей, радиусы которых относятся между собой, как числа Фибоначчи. Обычная для математики история.

Математический объект возникает в результате решения какой-нибудь математической задачи, исследуется математиками по законам логики и возникает перед их мысленным взором во всей красе. И тут, словно по мановению волшебной палочки, обнаруживается в самых разнообразных областях природы и жизни. Благодаря этому странному свойству математики возникла теоретическая физика, которая строит математические модели природы и с помощью этих моделей предсказывает новые физические эффекты.