Почему теорема Ферма - великая?

Известный нам по школьным учебникам Пифагор считал даже, что математика — она превыше всех человеческих чувств, даже любви. В общем, тем еще мистиком был автор теоремы про «пифагоровы штаны», недаром половину жизни он провел в Египте, обучаясь у тамошних жрецов.

Но как бы то ни было, самая известная математическая теорема — теорема Пифагора.

Впрочем, в математике есть еще одна, не менее знаменитая теорема, носящая имя человека. Человек этот теорему своего имени сформулировал, но не доказал, хотя думал, что доказал.

Пьер Ферма́ (Pierre de Fermat; 1601 —1665), французский известный математик, задал человечеству загадку, которую оно не смогло разгадать в течение 350 лет. Поэтому недаром эта теорема называется великой теоремой Ферма́. Формулировка теоремы простая и понятная любому, кто выучил начальный курс математики. Вот она:

Для любого натурального n>2 уравнение

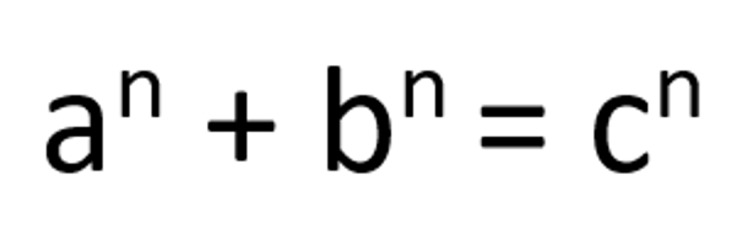
не имеет решений в целых ненулевых числах a, b, c.

А вот с этого места расскажем поподробнее.

Все начинается с уже упомянутой теоремы Пифагора. Уравнение, соответствующее этой теореме

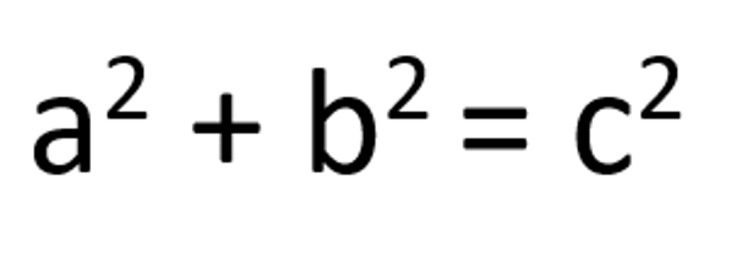
где a, b и c — натуральные числа, решение имеет. И одно из этих решений не трудно отыскать устно:

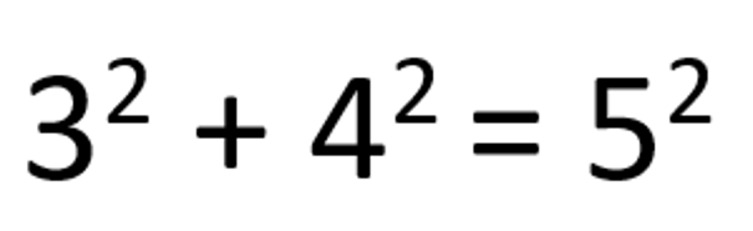
Таким образом, натуральное число, квадрат которого равен сумме квадратов двух других натуральных чисел, существует. А вот натурального числа, куб которого был бы равен сумме кубов двух других натуральных чисел, найти невозможно. Это же утверждение является верным для любых других степеней: 4, 5, 6…

Никаких заумных или непонятных слов в формулировке теоремы Ферма нет. Ее поймет даже школьник. Задача приманивает своей простотой. «Да неужели я не смогу решить столь простую задачу?» — думает каждый. И — вдохновленные простотой — многие впрягались в неподъемный воз.

То, что воз — неподъемный, ученые математики, попытавшиеся доказать великую теорему Ферма, стали догадываться очень скоро. В течение более чем трех столетий теорему Ферма доказали для различных частных случаев. Но общего доказательства для любых показателей степени в загадочном уравнении так и не было найдено. Теорема Ферма стала математическим аналогом вечного двигателя, который стремились изобретать все, кому было не лень и кто не знал о существовании закона сохранения энергии, согласно которому изобрести вечный двигатель было невозможно.

Но, в отличие от изобретения вечного двигателя, теорему Ферма доказать было можно и нужно. Кому нужно? Да в первую очередь самим математикам. Ведь в математике нет и быть не может недоказуемых теорем. Другое дело, что простая задачка оказалась слишком сложной.

Только в 1994 году великую теорему Ферма доказал английский ученый Эндрю Уайлс. За это выдающееся достижение Эндрю Уайлс в 2016 году стал лауреатом Абелевской премии, которая среди математиков столь же уважаема, как Нобелевская премия у представителей естественных наук, физики, химии и биологии.

Хотите узнать, как он добился победы? Об этом можно прочесть в прекрасной книге английского математика и популяризатора науки Саймона Сингха «Великая теорема Ферма».

С. Сингх понятно и захватывающе рассказывает о решении великой теоремы Ферма, которая, хотя и оказалась очень сложной математической задачей, породила в ходе попыток своего решения множество интересных разделов науки и, в конце концов, позволила математикам лучше понять, чем же, собственно говоря, являются числа.

А кем же был сам Пьер Ферма, сумевший походя сформулировать эту выдающуюся проблему?

Он родился в 1601 году в Гаскони в семье состоятельного торговца. Благодаря тому, что у отца было достаточно денег, Ферма смог получить образование. Он учился в университетах Тулузы, Бордо и Орлеана и получил диплом юриста.

Юриспруденция стала его кормилицей до конца жизни. С дипломом юриста Ферма стал членом высшего королевского суда в городе Тулузе. Затем он занял высокую судебную должность в городе Кастр, что неподалеку от Тулузы. Здесь же, в Кастре, Пьер Ферма скончался в январе 1665 года.

Писатель Чехов говорил, что медицина — его законная жена, а литература — любовница. Точно так же и Пьер Ферма делил время между судебными делами, которые он исполнял профессионально и точно, и занятиями математикой, на которую у него хватало и времени, и ученого пыла.

Ферма, будучи выдающимся ученым, книг по математике, между тем, не писал. Зато он переписывался с выдающимися учеными своего времени, такими как Р. Декарт и Б. Паскаль. В этих письмах он излагал свои идеи и решения различных математических задач, которые до него считались неразрешимыми. Именно благодаря своим письмам Ферма получил признание как гениальный математик. В одну книгу переписку Пьера Ферма собрал после его смерти сын. Собрал и издал. Так труды Ферма стали известны широкой научной общественности. Тогда же стала известна математикам великая теорема Ферма.

В отличие от Галилея или Ньютона, Ферма не занимался натуральной философией, то есть физикой. В отличие от Декарта и Паскаля, он не интересовался философией. Его интересом была только математика. Зато здесь он добился выдающихся успехов. Независимо от Декарта, Ферма создал аналитическую геометрию, раньше Ньютона он подобрался к методам дифференциального исчисления. Но главной его заслугой было создание теории чисел.

Теорию чисел называют еще высшей арифметикой. Смешное название для тех, кто думал, что арифметика настолько проста, что ее учат только в младших классах школы. На самом деле, решение сложных арифметических задач приводило математиков к самым основам их науки. Ведь, строго говоря, математики до сих пор не могут дать внятного определения того, что же представляет собой число. Точно так же, как физики до сих пор не могут четко сказать, как устроен мир. Но если физики для решения своих проблем строят могучие технические устройства-ускорители частиц, математикам нужны только карандаш да бумага. Ну, и, главное, умная голова на плечах.